电子信息技术(三)——数字电路
前言:
通过上期对电子信息技术简史的回顾,大家应该对电子信息技术的技术发展脉络有了基本的了解,那这期
我们了解一下数字电路。
不对啊,不应该先聊“电子信息技术(二)——模拟电路”么?
据我个人理解,模拟电路应该是数字电路的基础,但模拟电路水太深了,不敢在此班门弄斧,如果有模电 的大牛,可以将“模拟电路”这章补上。
言归正传,数字电路是现代信息技术的基础,学过数字电路的小伙伴应该记得,数字电路知识体系比较庞 大,在大学也是用两个学期才能学完,但今天我们主要了解如下几个概念:二进制、逻辑运算、组合逻辑电路、时序逻辑 电路。
不对啊,不应该先聊“电子信息技术(二)——模拟电路”么?
据我个人理解,模拟电路应该是数字电路的基础,但模拟电路水太深了,不敢在此班门弄斧,如果有模电 的大牛,可以将“模拟电路”这章补上。
言归正传,数字电路是现代信息技术的基础,学过数字电路的小伙伴应该记得,数字电路知识体系比较庞 大,在大学也是用两个学期才能学完,但今天我们主要了解如下几个概念:二进制、逻辑运算、组合逻辑电路、时序逻辑 电路。
一、二进制
大家平时生活中接触的主要是十进制计数,即逢十进一,二进制计数同理,逢二进一。二进制数据是用0
和1两个数码来表示的数。它的基数为2,进位规则是“逢二进一”,借位规则是“借一当二”。
将二进制引入电子技术可以说是一个开创性的杰作,我们了解半导体电路的高低电平有高低之分,二进制 的引入就是将高电平抽象为二进制数1,将低电平抽象为0,从此电子技术进入数字电路时代,数字电路可以计算二进制数 字,当今世界最复杂的数字电路当属CPU。
将二进制引入电子技术可以说是一个开创性的杰作,我们了解半导体电路的高低电平有高低之分,二进制 的引入就是将高电平抽象为二进制数1,将低电平抽象为0,从此电子技术进入数字电路时代,数字电路可以计算二进制数 字,当今世界最复杂的数字电路当属CPU。
二、逻辑运算
既然引进了二进制计数,那这些数据就需要进行计算,十进制数中常用的加、减、乘、除这些运算被称为
算数运算,二级制数同样可以进行算数运算,但同事二进制为数据的逻辑运算带来了便利。
逻辑运算又称布尔运算, 用等式表示判断,把推理看作等式的变换。
表示方式:
"∨" 表示"或"
"∧" 表示"与"
"┐"表示"非"
"=" 表示"等价"
1和0表示"真"和"假"
在逻辑代数中,有与、或、非三种基本逻辑运算。表示逻辑运算的方法有多种,如语句描述、逻辑代数式、 真值表、卡诺图等。逻辑运算中有逻辑常量和逻辑变量两个概念,逻辑常量只有两个,即0和1,用来表示两个对立的逻辑 状态。逻辑变量与普通代数一样,也可以用字母、符号、数字及其组合来表示,但它们之间有着本质区别,因为逻辑常量的 取值只有两个,即0和1,而没有中间值。
逻辑运算又称布尔运算, 用等式表示判断,把推理看作等式的变换。
表示方式:
"∨" 表示"或"
"∧" 表示"与"
"┐"表示"非"
"=" 表示"等价"
1和0表示"真"和"假"
在逻辑代数中,有与、或、非三种基本逻辑运算。表示逻辑运算的方法有多种,如语句描述、逻辑代数式、 真值表、卡诺图等。逻辑运算中有逻辑常量和逻辑变量两个概念,逻辑常量只有两个,即0和1,用来表示两个对立的逻辑 状态。逻辑变量与普通代数一样,也可以用字母、符号、数字及其组合来表示,但它们之间有着本质区别,因为逻辑常量的 取值只有两个,即0和1,而没有中间值。
三、组合逻辑电路和时序逻辑电路
数字电路根据逻辑功能的不同特点,可以分成两大类,一类叫组合逻辑电路(组合电路),另一类叫做时
序逻辑电路(时序电路)。
3.1 组合电路
组合电路:输出值只与当时的输入值有关,即输出惟一地由当时的输入值决定。与电路原来的状态无关,电路
没有记忆功能,输出状态随着输入状态的变化而变化,类似于电阻性电路。
其逻辑函数见下图:
其逻辑函数见下图:
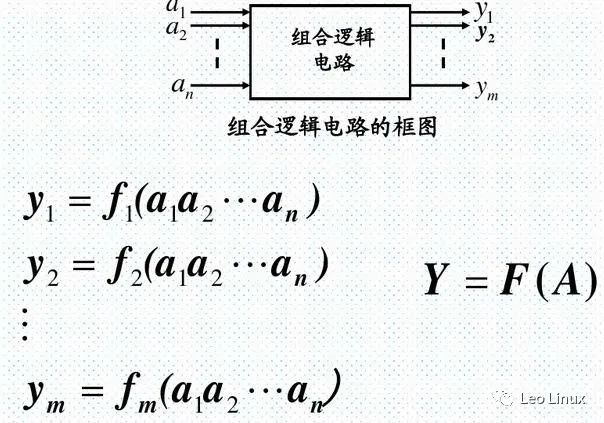
其中,a1-an为输入变量,y1-ym为输出变量。组合逻辑电路的特点归纳如下:
① 输入、输出之间没有返馈延迟通道;
② 电路中无记忆单元。
3.2 时序电路
时序电路:在逻辑功能上的特点是任意时刻的输出不仅取决于当时的输入信号,而且还取决于电路原来的状
态,或者说,还与以前的输入有关,其相当于在组合逻辑的输入端加上了一个反馈输入,在其电路中有一个
存储电路,其可以将输出的状态保持住。其结构形式见下图:
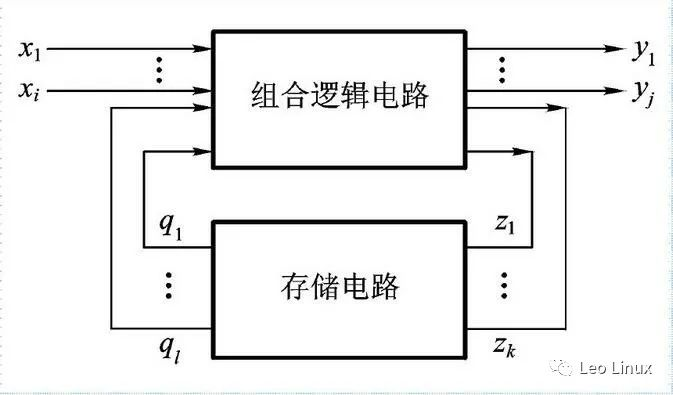
3.2.1 时序逻辑电路的组成:
1) 驱动方程:(激励方程) 很简单时可默认不写 。
Y=F(X,Qn)
2) 状态方程:将触发器特征方程改造而成的触发器的次态输出Qn+1与现态输出Qn的关系。
Qn+1=H(Z,Qn)
3) 输出方程:电路最终输出与触发器输出Qn的关系。
Y=F(X,Qn)
Y=F(X,Qn)
2) 状态方程:将触发器特征方程改造而成的触发器的次态输出Qn+1与现态输出Qn的关系。
Qn+1=H(Z,Qn)
3) 输出方程:电路最终输出与触发器输出Qn的关系。
Y=F(X,Qn)
三种方程中,驱动方程、状态方程最重要,输出方程往往可以不要,因为电路简单时,触发器的输出Qn一般就是
电路的最终输出。
3.2.2 时序电路分类
1)时序电路分为同步时序电路和异步时序电路:
同步时序电路:触发器状态的变化都是同一时钟操作下同时发生的。
异步时序电路:触发器状态的变化不是同时发生的。
2)时序电路分为米利(Mealy)型和摩尔(Moore)型:
米利型(Mealy):输出信号取决于输入变量和存储电路的状态。
摩尔型(Moore):输出信号仅仅取决于存储电路的状态。(摩尔型是米利型的特例而已)
引用:
[1]阎石,《数字电子技术基础 (第五版) 》,高等教育出版社
电子信息技术(三)——数字电路
https://leo-hou.github.io/2022/02/06/电子信息技术(三)——数字电路/